
创建自己的小题库
搜索

正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)题库
题数
2000
考试分类
高中数学>正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]函数 【图片】的最小正周期为 .
参考答案:
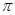
|
参考解析:
因为
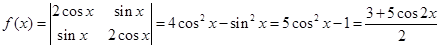 ,所以最小正周期为
,所以最小正周期为
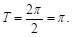
【简答题】

[2/2000]函数 【图片】是周期为 【图片】的周期函数吗?为什么?判断函数 【图片】是否为周期函数?
参考答案:
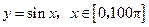 不是周期为 不是周期为
 的周期函数; 的周期函数;
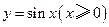 是周期为 是周期为
 的周期函数 的周期函数
|
参考解析:
不是周期函数,因为定义域中的
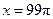 时,
时,
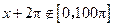 ,
,
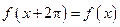 不能成立.函数
不能成立.函数
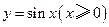 是周期为
是周期为
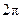 的周期函数.
的周期函数.
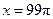 时,
时,
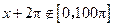 ,
,
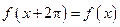 不能成立.函数
不能成立.函数
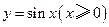 是周期为
是周期为
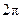 的周期函数.
的周期函数.
【简答题】

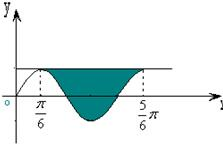
[3/2000]函数y=2sin3x( π6≤x≤ 5π6)与函数y=2的图象围成一个封闭图形,这个封闭图形的面积是 ______. 【图片】
参考答案:
| 根据正弦函数的对称性可得, 曲线从x=
把x轴下方的阴影部分补到x轴上方 ∴函数y=2sin3x的图象与函数y=2的图象围成一个封闭图形可转化为以2及
所求的面积S=
故答案为:
 |
参考解析:
无
【简答题】

[4/2000]已知函数f(x)=2sinωx(ω>0)在区间[- 【图片】, 【图片】]上的最小值为-2,则ω的取值范围是 .
参考答案:
|
[
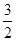 ,+∞). ,+∞).
|
参考解析:
因为
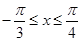 ,则
,则
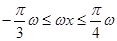 ,令
,令
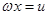 (其中
(其中
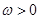 ),以下考虑函数
),以下考虑函数
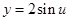 ,如图,
,如图,
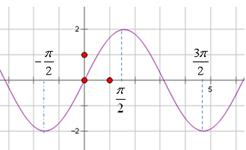 ,此时
,此时
 且
且
 ,则按题目要求,只需:
,则按题目要求,只需:
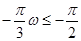 或
或
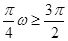 ,解得:
,解得:
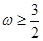 或
或
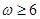 ,即
,即
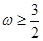 .
.
【简答题】

[5/2000]已知函数f(x)=cos(2x+ π2 )(x∈R),下面结论错误的是( ) A.函数f(x)的最小正周期为πB.函数f(x)是奇函数C....
参考答案:
函数f(x)=cos(2x+
函数在[0,
故选D. |
参考解析:
无
【简答题】

[6/2000]函数y=1-sinx(x∈R)的单调减区间是______.
参考答案:
由函数y=sinx的性质知,其在区间 [2kπ-
函数y=1-sinx(x∈R)的单调减区间是[2kπ-
故答案为:[2kπ-
|
参考解析:
无
【简答题】

[7/2000]函数f(x)=sin(2x+ 【图片】)图象的对称轴方程可以为( ) A.x= 【图片】B.x= 【图片】C.x= 【图片】D.x= 【图片】
参考答案:
|
A
|
参考解析:
对于函数
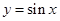 的对称轴方程为
的对称轴方程为
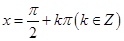 ,则令
,则令
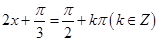 ,解得函数
,解得函数
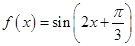 的对称轴方程为
的对称轴方程为
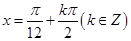 ,当
,当
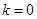 ,有
,有
 .所以正确答案为A.
.所以正确答案为A.
【简答题】

[8/2000]已知函数 【图片】(1)求函数 【图片】的最小正周期和单调递减区间; (2)在 【图片】中, 【图片】分别是角A、B、C的对边,若 【图片】,求 【图...
参考答案:
|
(1)
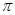 , ,
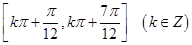 ;(2) ;(2)
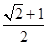
|
参考解析:
(1)利用两角和的正弦公式把
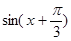 展开,再利用二倍角余弦、正弦公式对
展开,再利用二倍角余弦、正弦公式对
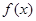 的解析式
的解析式
进行变形,可得
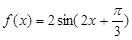 ,然后根据周期公式及正弦函数的单调性去求
,然后根据周期公式及正弦函数的单调性去求
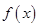 的最小正周期和
的最小正周期和
单调递减区间;(2) 由由已知得
 ,解出
,解出
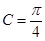 ,再由余弦定理结合基本不等式得
,再由余弦定理结合基本不等式得
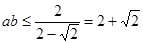 ,又
,又
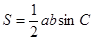 ,从而求出
,从而求出
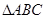 面积的最大值。
面积的最大值。
(1)函数

=
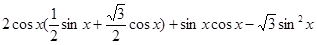
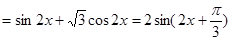 ,
,
所以函数
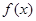 的最小正周期为
的最小正周期为
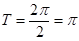 ,
,
由
 得
得
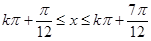 ,
,
即单调减区间为
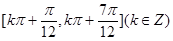 。
。
(2)由
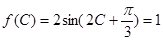 得
得
 ,由于C是
,由于C是
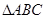 的内角,
的内角,
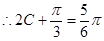 ,故
,故
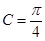 ,
,
由余弦定理得
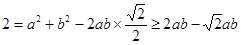 ,
,
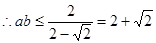 (当且仅当
(当且仅当
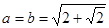 时取等号),
时取等号),
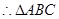 面积的最大值为
面积的最大值为
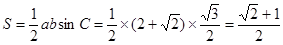 。
。
【简答题】

[9/2000](本题12分) 已知向量 【图片】, 【图片】且满足 【图片】. (1)求函数 【图片】的解析式和单调增区间; (2)锐角 【图片】中,若 【图片】,...
参考答案:
|
(1)略 (2) 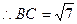
|
参考解析:
解(1)
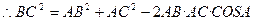

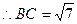
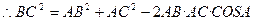

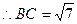
【简答题】

[10/2000]满足sin(x-π4)≥ 12的x的集合是( ) A.{x|2kπ+ 512π≤x≤2kπ+ 1312π,k∈Z}B.{x|2kπ- π12≤x≤2...
参考答案:
由sin(x-
解得 2kπ+
故选A. |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





