创建自己的小题库
搜索
合情推理题库
题数
1425
考试分类
高中数学>合情推理
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-合情推理
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/1425]在Rt△ABC中，若∠C=90°，AC=b，BC=a，则△ABC外接圆半径r= a2+b22．运用类比方法，若三棱锥的三条侧棱两两互相垂直且长度分别为...
参考答案：
直角三角形外接圆半径为斜边长的一半，由类比推理可知若三棱锥的三条侧棱两两互相垂直且长度分别为a，b，c，将三棱锥补成一个长方体，其外接球的半径R为长方体对角线长的一半．故为
故答案为：
|
参考解析：
| a2+b2+c2 |
【简答题】
[2/1425]“金导电、银导电、铜导电、铁导电，所以一切金属都导电”．此推理方法是（ ） A．完全归纳推理B．类比推理C．归纳推理D．演绎推理
参考答案：
| 因为金导电、银导电、铜导电、铁导电，而金、银、铜、铁等金属原子的核外价电子，在常温下都被激发到导带上，成为可自由移动的载流子，金属就是靠这些可自由移动的载流子导电的，由此类比得到一切金属都导电． 则“金导电、银导电、铜导电、铁导电，所以一切金属都导电”属于类比推理方法． 故选B． |
参考解析：
无
【简答题】
[3/1425]已知函数f（x）= 【图片】（x>0），如下定义一列函数：f1（x）=f（x），f2（x）=f（f1（x）），f3（x）=f（f2（x）），……...
参考答案：
 |
参考解析：
无
【简答题】
[4/1425]平面内一条直线把平面分成2部分，2条相交直线把平面分成4部分，1个交点；3条相交直线最多把平面分成7部分，3个交点；试猜想：n条相交直线最多把平面分成...
参考答案：
|
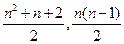
参考解析：
画出图形可知，4条相交直线最多可以把空间分成11，6个交点，5条相交直线最多可以把空间分成16，10个交点，归纳、猜想可得答案.
【简答题】
[5/1425]观察：① 【图片】； ② 【图片】，由此猜出一个一般式为 ．
参考答案：
|
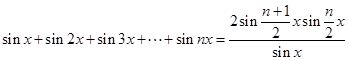
参考解析：
对比两个等式发现，左边和式中函数名称一致均为正弦，角的规律分别是10°的倍数、直到20倍，12°的倍数、直到16倍，右边分式结构相同，只有角不同，重点研究分子角的规律，所以猜想
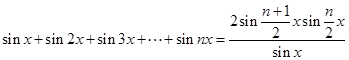
点评：分析两个式子的结构特点，结合数列知识，做出猜想。
【简答题】
[6/1425]将侧棱相互垂直的三棱锥称为“直角三棱锥”，三棱锥的侧面和底面分别叫直角三棱锥的“直角面和斜面”；过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”...
参考答案：
|
斜面的中面面积等于斜面面积的1/4
|
参考解析：
解：根据题意，可得实施类比的思路：点变成线，线变成面，从二维平面转变到三维空间；
（1）直角三角形具有性质：“两条直角边边长的平方和等于斜边边长的平方”，可得
以下性质：直角三棱锥中，三个直角面面积的平方和等于斜面面积的平方；
（2）直角三角形具有性质：“斜边的中线长等于斜边边长的一半”，可得
以下性质：直角三棱锥中，斜面的中面面积等于斜面面积的四分之一．
故答案为：直角三棱锥中，三个直角面面积的平方和等于斜面面积的平方
直角三棱锥中，斜面的中面面积等于斜面面积的四分之一
（1）直角三角形具有性质：“两条直角边边长的平方和等于斜边边长的平方”，可得
以下性质：直角三棱锥中，三个直角面面积的平方和等于斜面面积的平方；
（2）直角三角形具有性质：“斜边的中线长等于斜边边长的一半”，可得
以下性质：直角三棱锥中，斜面的中面面积等于斜面面积的四分之一．
故答案为：直角三棱锥中，三个直角面面积的平方和等于斜面面积的平方
直角三棱锥中，斜面的中面面积等于斜面面积的四分之一
【简答题】
[7/1425]把正偶数按下面的数阵排列， 2 4 6 8 10 12 14 16 ...
参考答案：
|
876
|
参考解析：
略
【简答题】
[8/1425]某校对文明班的评选设计了 【图片】五个方面的多元评价指标，并通过经验公式样 【图片】来计算各班的综合得分， S的值越高则评价效果越好，若某班在自测过程...
参考答案：
|
c
|
参考解析：
【解题思路】从分式的性质中寻找S值的变化规律.
因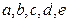
都为正数，故分子越大或分母越小时， S的值越大，而在分子都增加1的前提下，分母越小时，S的值增长越多，
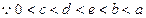，所以c增大1个单位会使得
S的值增加最多
【名师指引】此题的大前提是隐含的，需要经过思考才能得到
因
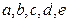都为正数，故分子越大或分母越小时， S的值越大，而在分子都增加1的前提下，分母越小时，S的值增长越多，
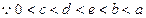，所以c增大1个单位会使得
S的值增加最多
【名师指引】此题的大前提是隐含的，需要经过思考才能得到
【简答题】
[9/1425]有如下结论：“圆x2+y2=r2上一点P（x0，y0）处的切线方程为x0y+y0y=r2”，类比也有结论：“椭圆x2a2+ y2b2=1（a＞b＞0）...
参考答案：
设M（2，t）（t∈R），A（x1，y1），B（x2，y2），则MA的方程为
∵点M在MA上，∴x1+ty1=1①，同理可得x2+ty2=1 ② 由①②知AB的方程为 x+ty=1，即x-1=ty ∴直线AB恒过一定点（1，0） 故答案为（1，0） |
参考解析：
x1x2
【简答题】
[10/1425]给出如下三角形数表： 【图片】此数表满足：①第n行首尾两数均为n，②表中数字间的递推关系类似于杨辉三角，即除了“两腰”上的数字以外，每一个数都等于它上...
参考答案：
| 由图可知：第n（n≥2）行第n-1个数等于故第n（n≥2）行第2个数 第二行的第二个数为2 第三行的第二个数为4=2+2 第四行的第二个数为7=3+2+2 第五行的第二个数为11=4+3+2+2 第六行的第二个数为16=5+4+3+2+2 … 故推断第n行的第二个数为：[（n-1）+（n-2）+…+2]+2=
故第n（n≥2）行第n-1个数等于
故答案为：第n（n≥2）行第n-1个数等于 |
参考解析：
n2-n+22
