
创建自己的小题库
搜索

相互独立事件同时发生的概率题库
题数
279
考试分类
高中数学>相互独立事件同时发生的概率
售价
¥20
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-相互独立事件同时发生的概率
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/279]某服务部门有n个服务对象,每个服务对象是否需要服务是独立的,若每个服务对象一天中需要服务的可能性是p,则该部门一天平均需服务的对象个数是( ...
参考答案:
| B |
参考解析:
无
【简答题】

[2/279]某射手进行射击训练,假设每次射击击中目标的概率为 【图片】,且每次射击的结果互不影响,已知射手射击了5 次,求: (1)其中只在第一、三、五次击中目标...
参考答案:
|
(1)
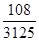 ;(2) ;(2)
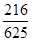 . .
|
参考解析:
(1)由题意可知,该射手在一、三、五次击中目标,在二、四次未击中目标,而每次射击的结果互不影响,因此由概率乘法公式可知所求概率为
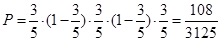 ;(2)该射手射击了
;(2)该射手射击了
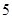 次,其中恰有
次,其中恰有
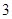 次击中目标,符合
次击中目标,符合
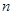 次独立重复试验恰发生
次独立重复试验恰发生
 次概率模型,根据二项分布相关内容,可知故所求概率为
次概率模型,根据二项分布相关内容,可知故所求概率为
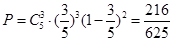 .
.
(1)该射手射击了
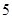 次,其中只在第一、三、五次击中目标,是在确定的情况下击中目标
次,其中只在第一、三、五次击中目标,是在确定的情况下击中目标
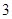 次,也即在第二、四次没有击中目标,所以只有一种情况,又各次射击的结果互不影响,
次,也即在第二、四次没有击中目标,所以只有一种情况,又各次射击的结果互不影响,
故所求其概率为
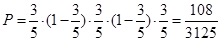 ;
;
(2)该射手射击了
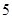 次,其中恰有
次,其中恰有
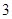 次击中目标,符合独立重复试验概率模型,
次击中目标,符合独立重复试验概率模型,
故所求其概率为
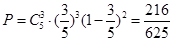 .
.
【简答题】

[3/279]同时投掷三颗骰子,于少有一颗骰子掷出6点的概率是 (结果要求写成既约分数).
参考答案:
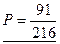
|
参考解析:
考虑对立事件,
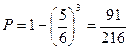 .
.
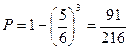 .
.
【简答题】

[4/279]某会议室用3盏灯照明,每盏灯各使用节能灯棍一只,且型号相同.假定每盏灯能否正常照明只与灯棍的寿命有关,该型号的灯棍寿命为1年以上的概率为0.8,寿命为...
参考答案:
| 解:(Ⅰ)设在第一次更换灯棍工作中,不需要更换灯棍的概率为P1, 则  ; ;(Ⅱ)对该盏灯来说,第1、2次都更换了灯棍的概率为  ; ;第一次未更换灯棍而第二次需要更换灯棍的概率为0.8(1-0.3), 故所求概率为:  。 。(Ⅲ)ξ的可能取值为0,1,2,3, 某盏灯在第二次灯棍更换工作中需要更换灯棍的概率为p=0.6,  , , , , , , , ,∴ξ的分布列为
∴  。 。
|
参考解析:
ξ
0
1
2
3
P




【简答题】

[5/279](文)在某次普通测试中,为测试汉字发音水平,设置了10张卡片,每张卡片上印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音“g”. (I)现对三位...
参考答案:
|
(I)
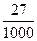 (Ⅱ) (Ⅱ)
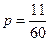
|
参考解析:
(I)记第一位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
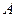 ,则
,则
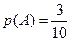 。记第二位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
。记第二位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
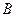 ,则
,则
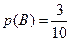 。记第三位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
。记第三位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
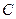 ,则
,则
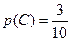 。又
。又
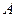 ,
,
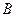 ,
,
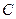 相互独立则这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”是
相互独立则这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”是
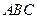 所以
所以
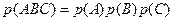
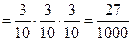
(Ⅱ)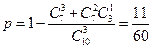
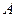 ,则
,则
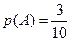 。记第二位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
。记第二位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
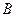 ,则
,则
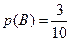 。记第三位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
。记第三位被测试者抽取的卡片上,拼音都带有后鼻音“g”为事件
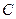 ,则
,则
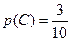 。又
。又
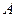 ,
,
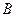 ,
,
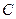 相互独立则这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”是
相互独立则这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”是
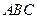 所以
所以
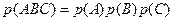
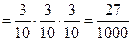
(Ⅱ)
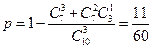
【简答题】

[6/279]一批产品需要进行质量检验,质检部门规定的检验方案是:先从这批产品中任取3件作检验,若3件产品都是合格品,则通过检验;若有2件产品是合格品,则再从这批产...
参考答案:
|
(1):
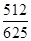 ;(2) ;(2)
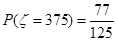 , ,
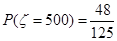 , ,
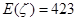 . .
|
参考解析:
(1):这是一道概率题,根据题意通过的情况有两种可能,每种情形可看成一个相互独立事件,则可得概率为两者之和,即:
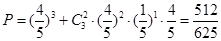 ;(2)中根据题意两种取值可能,即:
;(2)中根据题意两种取值可能,即:
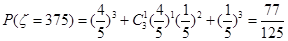 ,
,
 ,再根据概率公式即可计算出数学期望值:
,再根据概率公式即可计算出数学期望值:
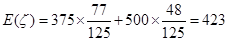 .
.
(1):
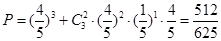 ; 5分
; 5分
(2)
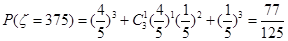 ,
,
 ,
,
∴
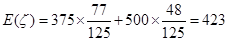 . 10分
. 10分
【简答题】

[7/279]某射击小组有甲、乙两名射手,甲的命中率为 【图片】,乙的命中率为P2,在射击比武活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中次数相等...
参考答案:
解:(1)  ; ;(2)该小组在一次检测中荣获“先进和谐组”的概率   而ξ~B(12,P),所以Eξ=12P 由Eξ≥5知  ·12≥5,且0≤P≤1, ·12≥5,且0≤P≤1,解得:  。 。 |
参考解析:
无
【简答题】

[8/279]某人射击1次,命中7~10环的概率如下表所示: 命中环数10环9环8环7环概率0.120.180.280.32 则该人射击一次,至少命中9...
参考答案:
|
0.3
|
参考解析:
略
【简答题】

[9/279]某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只...
参考答案:
解:(1)记“该生考上大学”的事件为A,其对立事件为 , ,则  , , ∴ 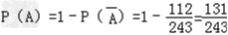 . .(2)记“该生参加测试的次数”为ξ,则ξ=4说明前3次考试只通过了1次, 而第4次通过了,或前4次都没有通过, 故 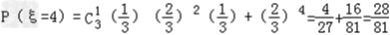 , , ξ=5说明前4次考试只通过了1次, 故 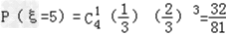 , ,∴该生至少参加四次考试的概率 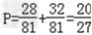 . . |
参考解析:
无
【简答题】

[10/279]中、日两国争夺某项国际博览会的申办权,进入最后一道程序,由国际展览局三名执委投票,决定承办权的最后归属。资 【图片】料显 【图片】示,A,B,C三名执...
参考答案:
|
(1)
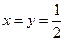 (2) (2)
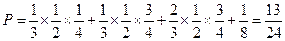
|
参考解析:
. 1)依题:
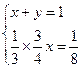 得
得
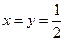
(2)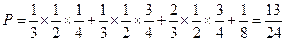
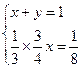 得
得
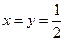
(2)
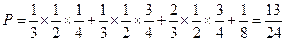

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





