
创建自己的小题库
搜索

等差数列的定义及性质题库
题数
2000
考试分类
高中数学>等差数列的定义及性质
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-等差数列的定义及性质
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]设等比数列 【图片】的公比 【图片】,前 【图片】项和为 【图片】,则 【图片】的值为 A. 【图片】B. 【图片】C. 【图片】D. 【图片】
参考答案:
|
A
|
参考解析:
本题考查等比数列的通项公式,前n项和公式和数列的基本运算.
因为等比数列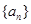 的公比
的公比
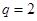 ,前
,前
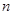 项和为
项和为
 ,所以
,所以
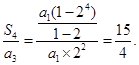 故选A
故选A
因为等比数列
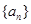 的公比
的公比
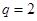 ,前
,前
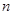 项和为
项和为
 ,所以
,所以
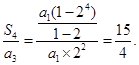 故选A
故选A
【简答题】

[2/2000]已知函数f(x)由下表定义 x 2 5 3 1 4 f(x) ∫π20sinxdx 2 3 4 5若a0=5,an+1=f(an),n∈N,则a201...
参考答案:
| ∵a0=5,∴a1=f(5)=2, ∴a2=f(2)=
=-cos
∴a3=f(1)=4, ∴a4=f(4)=5, 由以上可知:an+4=an,(n∈N), ∴a2012=a503×4+0=a0=5. 故答案为5. |
参考解析:
无
【简答题】

[3/2000]已知a、b、m、n、x、y均为正数,且a≠b,若a、m、b、x成等差数列,a、n、b、y成等比数列,则有( ) A.m>n,x>yB.m>n,x<y...
参考答案:
a、b、m、n、x、y均为正数,且a≠b,且 a、m、b、x成等差数列,∴m=
又 a、n、b、y成等比数列,∴n=
又 同理可得 b=
综上,m>n,x<y, 故选B. |
参考解析:
无
【简答题】

[4/2000]已知数列 【图片】中, 【图片】=2, 【图片】=1,若 【图片】为等差数列,则公差等于( ) A. 【图片】B. ...
参考答案:
|
D
|
参考解析:
由
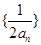 为等差数列,不妨设
为等差数列,不妨设
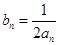 ,即
,即
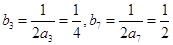 ,∴
,∴
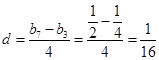 .
.
【简答题】

[5/2000]已知数列{ an}的首项a 【图片】=1,a 【图片】=a 【图片】+3(n≥2,n∈N 【图片】),则a 【图片】="( &n...
参考答案:
|
A
|
参考解析:
无
【简答题】

[6/2000]在数列{a n}中,若a 1=1,a n+1=a n+2(n≥1),则该数列的通项a n=________.
参考答案:
|
a
n=2n-1
|
参考解析:
无
【简答题】

[7/2000]设等差数列{an}的前n项和为Sn,若S15>0,S16<O,则S1a1,S2a2…S15a15中最大的是______.
参考答案:
由于S15=
S16=
所以可得a8>0,a9<0. 这样
而S1<S2<…<S8,a1>a2>…>a8, 所以在
故答案为:
|
参考解析:
无
【简答题】

[8/2000]已知等比数列{bn}的公比为3,数列{an}满足 【图片】,且a1=1。(1)判断{an}是何种数列,并给出证明;(2)若 【图片】,Tn是数列{Cn...
参考答案:
解:(1)数列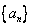 为等差数列; 为等差数列;证明:因为数列 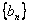 是公比为3的等比数列, 是公比为3的等比数列,所以, 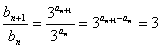 , ,所以, 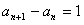 , ,即数列  是首项为1,公差为1的等差数列. 是首项为1,公差为1的等差数列.(2)由(1)可知 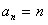 ,则 ,则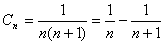 , ,于是 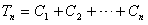  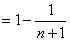 , , 由 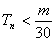 ,得 ,得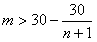 , , 而 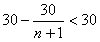 对所有n∈N*都成立,所以, 对所有n∈N*都成立,所以,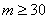 , ,所以,使得 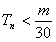 对所有n∈N*都成立的最小正整数m=30。 对所有n∈N*都成立的最小正整数m=30。 |
参考解析:
无
【简答题】

[9/2000]已知非零实数x,y,a,b,x,y分别为a与b,b与c的等差中项,且满足ax+ cy=2,求证:非零实数a,b,c成等比数列.
参考答案:
证明:由x,y分别为a与b,b与c的等差中项,得x=
代入已知等式:
所以非零实数a,b,c成等比数列. |
参考解析:
无
【简答题】

[10/2000]已知数列{an}中,a1=0,an+1=an•q+qn+1(q>0),bn=an+2n,n=1,2,3,….(I)求证数列{ anqn}是等差数列;(...
参考答案:
| (I)∵an+1=an•q+qn+1(q>0) ∴
即数列{
且
(II)bn=an+2n=(n-1)qn+2n(4分) ∴b1=2,b2=q2+4,b3=2q3+8(5分) ∴b22-b1b3=(q2+4)2-2(2q3+8)=(q4+8q2+16)-4q3-16=q4-4q3+8q2=q2(q2-4q+8)=q2[(q-2)2+4]>0 ∴b22>b1b3(8分) (III)∵bn=(n-1)qn+2n,n=1,2,3,…,∴bn>0 b1=2,b2=q2+4,bn+1=nqn+1+2n+1
又b2bn-b1bn+1=(q2+4)[(n-1)qn+2n]-2(nqn+1+2n+1) =[(q2+4)(n-1)-2nq]qn+q2•2n ①当n=1时,b2bn-b1bn+1=0,即
②当n≥2时,∵q>0,q2+4≥2•q•2=4q ∴(q2+4)(n-1)-2nq≥4(n-1)q-2nq=2(n-2)q≥0又q2•2n>0 ∴b2bn-b1bn+1>0 由①②得
故所求的正整数k=1. |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





