
创建自己的小题库
搜索

相似三角形的判定及有关性质题库
题数
205
考试分类
高中数学>相似三角形的判定及有关性质
售价
¥20
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-相似三角形的判定及有关性质
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/205]如图所示,四边形ABCD为矩形,点M是BC的中点,CN= 【图片】CA,用向量法证明: (1)D、N、M三点共线;(2)若四边形ABCD为正方形,则D...
参考答案:
|
(1)设
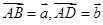
∵ 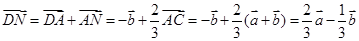
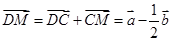 ………3分 ………3分
∴ 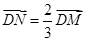 ,且DM与DN有公共点D ,且DM与DN有公共点D
∴D、N、M三点共线 (2)若四边形ABCD为正方形,则 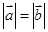 且 且
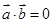
∵ 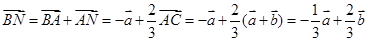
∴ 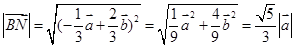
同理可得 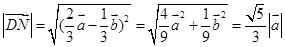 ∴ ∴
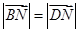 ,即DN=BN ,即DN=BN
备注:利用坐标来运算的相应得分. |
参考解析:
(1)用向量法证明可以选建立直角坐标系,用向量的坐标运算进行证明三点共线.
(2)线段长度相等就是证明其对应的向量的模相等即可,即证: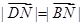 .
.
(2)线段长度相等就是证明其对应的向量的模相等即可,即证:
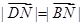 .
.
【简答题】

[2/205].在平行四边形ABCD中,AB=3,AD=2, 【图片】,E是DC的中点, F是AE的中点,则 【图片】= &nb...
参考答案:
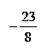
|
参考解析:
略
【简答题】

[3/205]如图所示,平行四边形ABCD中,AE∶EB=1∶2,若△AEF的面积等于1 cm 2,则△CDF的面积等于________cm 2. 【图片】
参考答案:
|
9
|
参考解析:
平行四边形ABCD中,有
 ,
,
所以,
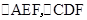 的面积之比等于对应边长之比的平方,
的面积之比等于对应边长之比的平方,
因为,
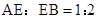 ,所以,
,所以,
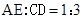 ,
,
因为,
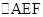 的面积等于1cm
2,
的面积等于1cm
2,
所以,
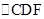 的面积等于9cm
2,故答案为9.
的面积等于9cm
2,故答案为9.
【简答题】

[4/205](选做题)如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:(1)∠DEA=∠DFA;(2)AB2=BE·BD...
参考答案:
| 证明:(1)连结AD,因为AB为圆的直径, 所以∠ADB=90°, 又EF⊥AB,∠EFA=90°, 则A、D、E、F四点共圆, ∴∠DEA=∠DFA; (2)由(1)知,BD·BE=BA·BF, 又△ABC∽△AEF, ∴  ,即AB·AF=AE·AC, ,即AB·AF=AE·AC,∴BE·BD-AE·AC=BA·BF-AB·AF=AB(BF-AF)=AB2。 |
 |
参考解析:
无
【简答题】

[5/205]如图:正方体ABCD—A 1B 1C 1D 1中,E、F、G、H、K、L分别为AB、BB 1、B 1C 1、C 1D 1、D 1D、DA的中点,则六边...
参考答案:
|
B
|
参考解析:
分析:由题意不难判断六边形EFGHKL在正方体面后、下面、右面上的射影,(前后、左右、上下的射影相同)即可得到结论.
解:E、F、G、H、K、L分别为AB、BB 1、B 1C 1、C 1D 1、D 1D、DA的中点,
则六边形EFGHKL在正方体后面上的射影,
在左侧面上的射影也应该是
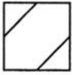 在底面ABCD上的投影为
在底面ABCD上的投影为
 即是B图,
即是B图,
故选B.
【简答题】

[6/205]如图, 【图片】是⊙ 【图片】的直径, 【图片】、 【图片】是⊙ 【图片】上的点, 【图片】是 【图片】的角平分线,过点 【图片】点作 【图片】,交 ...
参考答案:
|
证明:(1)连结
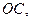
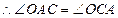 ,……2分 ,……2分
又 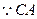 是 是
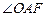 的角平分线, 的角平分线,
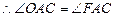 , ,
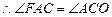 , ,
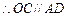 …4分 …4分
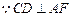 , ,
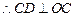 ,即 ,即
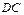 是圆 是圆
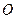 的切线 …6分 的切线 …6分
(2)连结 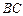 ,在 ,在
 中, 中,
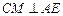 , ,
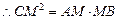 ………8分 ………8分
又 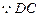 是圆 是圆
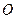 的切线, 的切线,
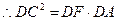
 ,易知 ,易知
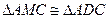 ………10分 ………10分

∴ 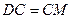 , ,
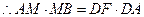 ………12分 ………12分
|
参考解析:
略
【简答题】

[7/205](选做题)如图,AB是 【图片】的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且 【图片】,求证: 【图片】 (1) 【图片】;(2)...
参考答案:
证明:(1)连接 ,在 ,在 中 中   又   ∽ ∽ 则   。 。(2)在  中, 中, 又    四点共圆; 四点共圆;  又  是⊙ 是⊙ 的直径,则 的直径,则 , ,   。 。 |
参考解析:
无
【简答题】

[8/205]如图,在正三角形ABC中,D、E分别在AC、AB上, 【图片】,AE=BE,则有( ) A.△AED∽△BED B.△AED∽△CBD C.△AED...
参考答案:
| B |
参考解析:
无
【简答题】

[9/205]如图,A,B,C,D四点在同一个圆上,BC与AD的延长线交于点E,点F在BA的延长线上。 【图片】 【图片】
参考答案:
| (1)解:∵A,B,C,D四点共圆 ∴∠EDC=∠EBF 又∵∠DEC=∠AEC ∴△ECD∽△EAB  又∵  ∴  (2)证明:∵EF2=FA·FB  又∵∠EFA=∠BFE ∴△FAE∽△FEB ∴∠FEA=∠EBF 又∵A,B,C,D四点共圆 ∴∠EDC=∠EBF ∴∠FEA=∠EDC ∴EF∥CD |
参考解析:
无
【简答题】

[10/205]如图,C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB平分线DC交AE于点F,交AB于D点.(I)求∠ADF的度数;(II)若AB=AC,求A...
参考答案:
| (I)∵AC为圆O的切线, ∴∠B=∠EAC 又知DC是∠ACB的平分线, ∴∠ACD=∠DCB ∴∠B+∠DCB=∠EAC+∠ACD 即∠ADF=∠AFD 又因为BE为圆O的直径, ∴∠DAE=90° ∴∠ADF=
(II)∵∠B=∠EAC,∠ACB=∠ACB, ∴△ACE∽△ABC ∴
又∵AB=AC, ∴∠B=∠ACB=30°,(8分) ∴在RT△ABE中,
|
参考解析:
12

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





