
创建自己的小题库
搜索

数学归纳法题库
题数
310
考试分类
高中数学>数学归纳法
售价
¥20
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-数学归纳法
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/310]求证 【图片】
参考答案:
| 证明: ①当n=1时,左边=2,右边=  ,等式成立; ,等式成立;②假设当n=k时,等式成立, 即  则当n=k+1时,左边=  =(k+1)(k+2)(  k+1)= k+1)= (k+1)(k+2)(k+3) (k+1)(k+2)(k+3)即n=k+1时,等式也成立. 所以  对任意正整数都成立. 对任意正整数都成立. |
参考解析:
无
【简答题】

[2/310]在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列,(Ⅰ)求a2,a3,a4及b2,...
参考答案:
解:(Ⅰ)由条件得 , ,由此可得  , ,猜测  , ,用数学归纳法证明: ①当n=1时,由上可得结论成立; ②假设当n=k时,结论成立,即  , ,那么当n=k+1时,  , ,所以当n=k+1时,结论也成立; 由①②,可知  对一切正整数都成立。 对一切正整数都成立。(Ⅱ)  , , n≥2时,由(Ⅰ)知  , ,故    , ,综上,原不等式成立. |
参考解析:
无
【简答题】

[3/310]已知n为正偶数,用数学归纳法证明 【图片】时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( ) A.n=k+1时等...
参考答案:
| B |
参考解析:
无
【简答题】

[4/310]首项为正数的数列{an}满足an+1= 【图片】(an2+3),n∈N*,(Ⅰ)证明:若a1为奇数,则对一切n≥2,an都是奇数;(Ⅱ)若对一切n∈N...
参考答案:
解:(Ⅰ)已知a1是奇数,假设 是奇数,其中m为正整数, 是奇数,其中m为正整数,则由递推关系得  是奇数。 是奇数。根据数学归纳法,对任何n∈N+,an都是奇数。 (Ⅱ)由  知, 知, ,当且仅当 ,当且仅当 ; ;另一方面,若  ,则 ,则 ; ;若  ,则 ,则 , ,根据数学归纳法,  ; ;综合所述,对一切n∈N+都有  的充要条件是 的充要条件是 。 。 |
参考解析:
无
【简答题】

[5/310]设数列a1,a2,…,an,…中的每一项都不为0,证明,{an}为等差数列的充分必要条件是:对任何n∈N+都有 【图片】。
参考答案:
| 证明:先证必要性: 设数列{an}的公差为d,若d=0,则所述等式显然成立; 若d≠0, 则 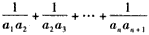 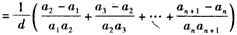 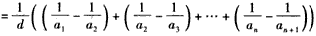 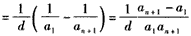 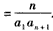 ; ;再证充分性:(数学归纳法)设所述的等式对一切n∈N+都成立, 首先,在等式 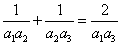 ,① ,① 两端同乘a1a2a3,即得a1+a3=2a2,所以a1,a2,a3成等差数列, 记公差为d,则a2=a1+d, 假设ak=a1+(k-1)d,当n=k+1时,观察如下二等式 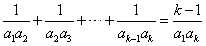 ,② ,② 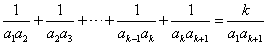 ,③ ,③将②代入③,得 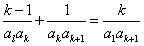 , ,在该式两端同乘a1akak+1,得(k-1) 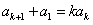 , ,将ak=a1+(k-1)d代入其中,整理,得ak+1=a1+kd, 由数学归纳法原理知,对一切n∈N+,都有an=a1+(n-1)d,所以{an}是公差为d的等差数列。 |
参考解析:
无
【简答题】

[6/310]函数 【图片】。定义数列 【图片】如下: 【图片】是过两点 【图片】的直线 【图片】与x轴交点的横坐标。(1)证明: 【图片】;(2)求数列 【图片】...
参考答案:
解:(1)因为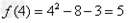 , ,故点  在函数 在函数 的图像上, 的图像上,故由所给出的两点 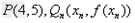 , ,可知,直线 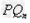 斜率一定存在。 斜率一定存在。故有直线 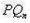 的直线方程为 的直线方程为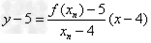 ,令 ,令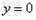 , ,可求得 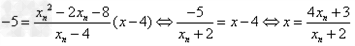 所以 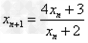 下面用数学归纳法证明 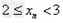 当 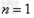 时, 时,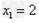 ,满足 ,满足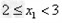 假设 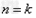 时, 时,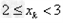 成立, 成立,则当 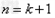 时, 时,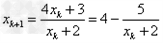 , ,由 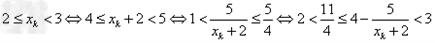 即 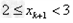 也成立 也成立综上可知 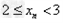 对任意正整数恒成立。 对任意正整数恒成立。下面证明 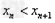 由 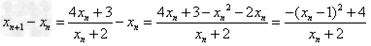 由 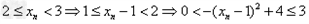 , ,故有 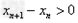 即 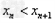 综上可知 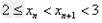 恒成立。 恒成立。(2)由 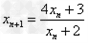 得到该数列的一个特征方程 得到该数列的一个特征方程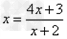 即 即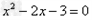 ,解得 ,解得 或 或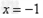  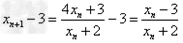 ① ① 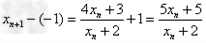 ② ②两式相除可得 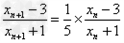 ,而 ,而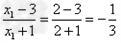 故数列 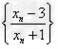 是以 是以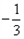 为首项以 为首项以 为公比的等比数列 为公比的等比数列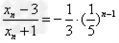 故 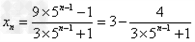 。 。 |
参考解析:
无
【简答题】

[7/310]已知数列{an}中, 【图片】(n∈N*),记 【图片】。(1)写出{bn}的前三项;(2)猜想数列{bn}的通项公式,并用数学归纳法证明;(3)令 ...
参考答案:
解:(1)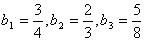 ; ;(2) 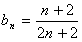 ; ;数学归纳法证明“略”; (3) 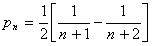 ; ;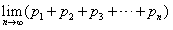 = =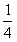 。 。 |
参考解析:
无
【简答题】

[8/310]用数学归纳法证明不等式2n>n2时,第一步需要验证n0=( )时,不等式成立. A.5 B.2和4 C.3 D.1
参考答案:
| A |
参考解析:
无
【简答题】

[9/310]用数学归纳法证明:x2n-1-y2n-1能被x-y整除.(n∈N*)
参考答案:
| 证:①当n=1时,结论显然成立. ②假设当n=k时结论成立,即x2k-1-y2k-1能被x-y整除 则当n=k+1时, x2k+1-y2k+1=x2x2k-1-y2y2k-1 =x2x2k-1-x2y2k-1+x2y2k-1-y2y2k-1 =x2(x2k-1-y2k-1)+(x2-y2)y2k-1 ∴x2k+1-y2k+1也能被x-y整除 故当n=k+1时结论也成立. 由①、②可知,对于任意的n∈N*,x2n-1-y2n-1能被x-y整除. |
参考解析:
无
【简答题】

[10/310]设数列{an}的前n项和为Sn,且S2n-2Sn-anSn+1=0,n=1,2,3,…。(1)求a1,a2;(2)求Sn的表达式。
参考答案:
解:(1)当n=1时,由已知得 , ,解得  , ,同理,可解得  。 。(2)由题设  当n≥2(n∈N*)时,  代入上式得  由(1)可得  由(*)可得  , ,由此猜想  , ,证明:①当n=1时,结论成立; ②假设当n=k(k∈N*)时结论成立, 即  , ,那么当n=k+1时,由(*)得  , ,∴  所以当n=k+1时结论也成立, 根据①和②可知,  对所有正整数n都成立, 对所有正整数n都成立,因此  。 。 |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





