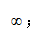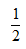设k(s，t)为单位正方形[0，1]×[0，1]上的纯量连续函数，k不恒为0，且任取s，t∈[0，1]有k(s，t)=k(t，s)。设A定义在L 2 [0，1]为 ，0≤s≤1，  x∈L 2 [0，1]。 求证：存在非零实序列{λ n }，存在由[0，1]上的连续函数组成的标准正交序列{u n }，使得对x∈L 2 [0，1] 其中，若上述级数为无穷级数，则这个级数对0≤s≤1一致收敛。证明∑|λ n | 2 ＜∞