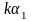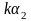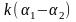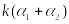创建自己的小题库
搜索
参考答案:


举一反三
【单选题】设p(x),q(x),f(x)均是x的连续函数,y1(x),y2(x),y3(x)是y"+p(x)y'+q(x)y=f(x)的3个线性无关的解,c1与c2是两个任意常数,则该非齐次方程的通解是 ( ).
A.
c1y1+(c2+c1)y2+(1-c2)y3.
B.
(c1-c1)yl+(c2-1)y2+(1-c1)y3.
C.
(c1+c2)y1+(c1-c2)y2+(1-c1)y3.
D.
c(1y1+c2y2+(1-c1-c2)y3.
【单选题】设m×n矩阵A的秩为R(A)=n-1,且ξ1,ξ2是齐次方程Ax=0的两个不同的解,则Ax=0的通解为()
A.
kξ1,k∈R
B.
kξ2,k∈R
C.
k(ξ1+ξ2),k∈R
D.
k(ξ1-ξ2),k∈R
【单选题】设ξ 1 ,ξ 2 是非齐次方程组AX=β的两个不同的解,η 1 ,η 2 为它的导出组AX=0的一个基础解系,则它的通解为( )
A.
k 1 η 1 +k 2 η 2 +(ξ 1 -ξ 2 )/2.
B.
k 1 η 1 +k 2 (η 1 -η 2 )+(ξ 1 +ξ 2 )/2.
C.
k 1 η 1 +k 2 (ξ 1 -ξ 2 )+(ξ 1 -ξ 2 )/2.
D.
k 1 η 1 +k 2 (ξ 1 -ξ 2 )+(ξ 1 +ξ 2 )/2.

相关题目:
【单选题】设p(x),q(x),f(x)均是x的连续函数,y1(x),y2(x),y3(x)是y"+p(x)y'+q(x)y=f(x)的3个线性无关的解,c1与c2是两个任意常数,则该非齐次方程的通解是 ( ).
A.
c1y1+(c2+c1)y2+(1-c2)y3.
B.
(c1-c1)yl+(c2-1)y2+(1-c1)y3.
C.
(c1+c2)y1+(c1-c2)y2+(1-c1)y3.
D.
c(1y1+c2y2+(1-c1-c2)y3.
【单选题】设m×n矩阵A的秩为R(A)=n-1,且ξ1,ξ2是齐次方程Ax=0的两个不同的解,则Ax=0的通解为()
A.
kξ1,k∈R
B.
kξ2,k∈R
C.
k(ξ1+ξ2),k∈R
D.
k(ξ1-ξ2),k∈R
【单选题】设ξ 1 ,ξ 2 是非齐次方程组AX=β的两个不同的解,η 1 ,η 2 为它的导出组AX=0的一个基础解系,则它的通解为( )
A.
k 1 η 1 +k 2 η 2 +(ξ 1 -ξ 2 )/2.
B.
k 1 η 1 +k 2 (η 1 -η 2 )+(ξ 1 +ξ 2 )/2.
C.
k 1 η 1 +k 2 (ξ 1 -ξ 2 )+(ξ 1 -ξ 2 )/2.
D.
k 1 η 1 +k 2 (ξ 1 -ξ 2 )+(ξ 1 +ξ 2 )/2.

参考解析:


AI解析
重新生成

题目纠错 0
发布


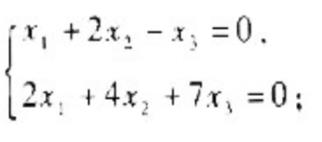

 分享
分享 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫 反馈
反馈 收藏
收藏 举报
举报