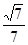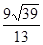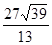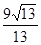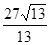创建自己的小题库
搜索
【简答题】


(本小题满分12分) 如图2,在直三棱柱ABC-
 中,AB=1,
中,AB=1,
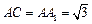 ,
,
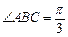 .
.
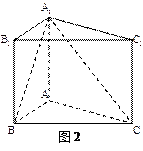 (Ⅰ)证明:
(Ⅰ)证明:
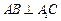 ; (Ⅱ)求二面角
; (Ⅱ)求二面角
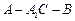 的正弦值.
的正弦值.

 分享
分享
 反馈
反馈 收藏
收藏 举报
举报参考答案:


举一反三
【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
【单选题】三棱柱ABC—A1B1C1中,AA1=1,AB=4,BC=3,∠ABC=90°,设平面A1BC1与平面ABC的交线为l,则A1C1与l的距离为( )
A.
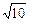
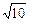
B.
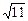
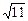
C.
2.6
D.
2.4
【单选题】类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的下列性质,你认为比较恰当的是 ①各棱长相等,同一顶点上的任两条棱的夹角相等;②各个面是全等的正三角形,相邻的两个面所成的二面角相等;③各个面都是全等的正三角形,同一顶点的任两条棱的夹角相等;④各棱长相等,相邻两个面所成的二面角相等。 [ ]
A.
①④
B.
①②
C.
①②③
D.
③

相关题目:
【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
【单选题】三棱柱ABC—A1B1C1中,AA1=1,AB=4,BC=3,∠ABC=90°,设平面A1BC1与平面ABC的交线为l,则A1C1与l的距离为( )
A.
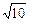
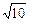
B.
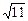
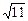
C.
2.6
D.
2.4
【单选题】类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的下列性质,你认为比较恰当的是 ①各棱长相等,同一顶点上的任两条棱的夹角相等;②各个面是全等的正三角形,相邻的两个面所成的二面角相等;③各个面都是全等的正三角形,同一顶点的任两条棱的夹角相等;④各棱长相等,相邻两个面所成的二面角相等。 [ ]
A.
①④
B.
①②
C.
①②③
D.
③

参考解析:


AI解析
重新生成

题目纠错 0
发布

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫