
创建自己的小题库
搜索
【单选题】


若
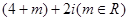 是纯虚数,则圆锥曲线
是纯虚数,则圆锥曲线
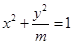 的离心率为( )
的离心率为( )
A.
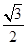
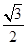
B.
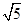
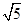
C.
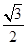 或
或
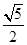
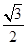 或
或
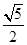
D.
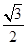 或
或
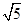
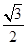 或
或
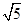

 分享
分享
 反馈
反馈 收藏
收藏 举报
举报参考答案:


举一反三
【单选题】已知P是双曲线x2a2-y2b2=1(a>0,b>0)上的点,F1、F2是其焦点,双曲线的离心率是54,且PF1?PF2=0,若△PF1F2的面积为9,则a+b的值为( )
A.
5
B.
6
C.
7
D.
8
【简答题】已知椭圆 x2 25 + y2 b2 =1(0<b<5)的离心率为 3 5 ,则b等于( )
A.
16
B.
8
C.
5
D.
4

相关题目:
【单选题】已知P是双曲线x2a2-y2b2=1(a>0,b>0)上的点,F1、F2是其焦点,双曲线的离心率是54,且PF1?PF2=0,若△PF1F2的面积为9,则a+b的值为( )
A.
5
B.
6
C.
7
D.
8
【简答题】已知椭圆 x2 25 + y2 b2 =1(0<b<5)的离心率为 3 5 ,则b等于( )
A.
16
B.
8
C.
5
D.
4

参考解析:


AI解析
重新生成

题目纠错 0
发布

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫




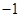

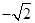
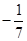
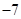 或
或





