创建自己的小题库
搜索
【简答题】
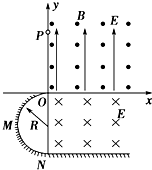
如图所示，竖直平面坐标系xOy的第一象限，有垂直：xOy面向外的水平勻强磁场和竖直向上的匀强电场，大小分别为B和E第四象限有垂直xOy為面向里的水平匀强电场，大小E'=2E 第三象限内有一绝缘光滑竖直放置的半径为R的半圆轨道，轨道最髙点与坐标原点O相切，最低点与绝缘光滑水平面相切于N．一质量为m的带电小球从y轴上（y＞0）的P点沿工轴正方向进入第一象限后做圆周运动，恰好通过坐标原点O，且水平切入半圆轨道并沿轨道内侧运动，过N点水平进入第四象限，并在电场中运动•（已知为g）（1）判断小球的带电性质并求出其所带电荷量．（2）P点距坐标原点O至少多高？（3）若该小球以满足（2）中OP最小值的位置和对应速度进入第一象限，通过N点开始计时，经时间t=2 R g ，小球距N点的距离s为多远？
手机使用
分享
复制链接
新浪微博
分享QQ
微信扫一扫
反馈
收藏
举报参考答案：
举一反三
【简答题】一个物体做自由落体运动，重力加速度g取10m/s2，则（ ）
A.
物体4s末的速度为40m/s
B.
物体4s末的速度为20m/s
C.
物体4s内下落的高度为160m
D.
物体4s内下落的高度为80m
【简答题】围绕地球做圆周运动的两颗卫星在空间某轨道上相撞，碰撞点比相对地球静止的国际空间站高434km．则（ ）
A.
在碰撞点高度运行的卫星的周期比国际空间站的周期大
B.
在碰撞点高度运行的卫星的向心加速度比国际空间站的向心加速度大
C.
两颗卫星在碰撞前均处于失重状态
D.
若发射一颗在碰撞点高度处运行的卫星，发射速度应大于11.2km/s
【多选题】关于匀速圆周运动的说法，正确的是（ ）
A.
匀速圆周运动的速度大小保持不变，所以做匀速圆周运动的物体没有加速度
B.
做匀速圆周运动的物体，虽然速度大小不变，但方向时刻都在改变，所以必有加速度
C.
做匀速圆周运动的物体，加速度的大小保持不变，所以是匀变速（曲线）运动
D.
匀速圆周运动的物体加速度大小虽然不变，但加速度的方向始终指向圆心，加速度的方向时刻都在改变，所以匀速圆周运动既不是匀速运动，也不是匀变速运动
相关题目：
【简答题】一个物体做自由落体运动，重力加速度g取10m/s2，则（ ）
A.
物体4s末的速度为40m/s
B.
物体4s末的速度为20m/s
C.
物体4s内下落的高度为160m
D.
物体4s内下落的高度为80m
【简答题】围绕地球做圆周运动的两颗卫星在空间某轨道上相撞，碰撞点比相对地球静止的国际空间站高434km．则（ ）
A.
在碰撞点高度运行的卫星的周期比国际空间站的周期大
B.
在碰撞点高度运行的卫星的向心加速度比国际空间站的向心加速度大
C.
两颗卫星在碰撞前均处于失重状态
D.
若发射一颗在碰撞点高度处运行的卫星，发射速度应大于11.2km/s
【多选题】关于匀速圆周运动的说法，正确的是（ ）
A.
匀速圆周运动的速度大小保持不变，所以做匀速圆周运动的物体没有加速度
B.
做匀速圆周运动的物体，虽然速度大小不变，但方向时刻都在改变，所以必有加速度
C.
做匀速圆周运动的物体，加速度的大小保持不变，所以是匀变速（曲线）运动
D.
匀速圆周运动的物体加速度大小虽然不变，但加速度的方向始终指向圆心，加速度的方向时刻都在改变，所以匀速圆周运动既不是匀速运动，也不是匀变速运动
参考解析：
AI解析
重新生成
题目纠错 0
发布
