
创建自己的小题库
搜索
【多选题】


设
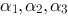 是
是
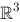 的一个标准正交基,下列向量组也是标准正交基的是( ).
的一个标准正交基,下列向量组也是标准正交基的是( ).
A.
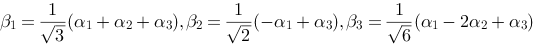
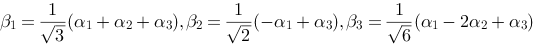
B.
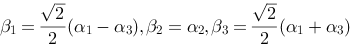
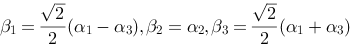
C.
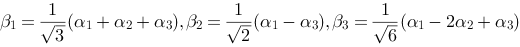
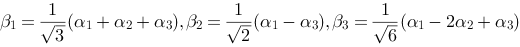
D.
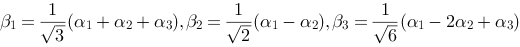
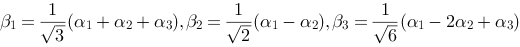

 分享
分享
 反馈
反馈 收藏
收藏 举报
举报参考答案:


举一反三
【单选题】下列向量线性相关的是
A.
(1,1,1),(1,1,0),(1,0,0)
B.
(2,1,0),(-1,3,1),(5,2,1)
C.
(7,4,1),(-2,1,2),(3,6,5)
D.
(-1,3,8),(-2,0,5),(2,1,9)
【单选题】已知4阶方阵A=[α 1 ,α 2 ,α 3 ,α 4 ],α 1 ,α 2 ,α 3 ,α 4 均为四维列向量,其中α 1 ,α 2 线性无关,若α 1 +2α 2 -α 3 =β,α 1 +α 2 +α 3 +α 4 =β,2α 1 +3α 2 +α 3 +2α 4 =β,k 1 ,k 2 为任意常数,那么Ax=β的通解为
A.
B.
A. 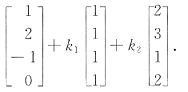
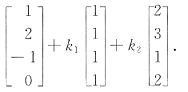
C.
B. 

D.
C. 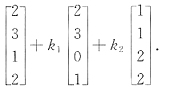
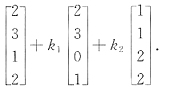
E.
D. 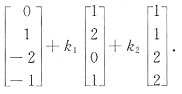
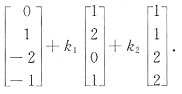
【单选题】设 a , b 是一组非正交的基底,为得到正交基底,可在集合 { a +t b |t∈R} 中找一个向量与 a 组成一组正交基底,根据上述要求,若 a =(1,2) , b =(2,3) ,则t的值为( )
A.
- 3 8
B.
- 5 11
C.
- 5 8
D.
- 7 9

相关题目:
【单选题】下列向量线性相关的是
A.
(1,1,1),(1,1,0),(1,0,0)
B.
(2,1,0),(-1,3,1),(5,2,1)
C.
(7,4,1),(-2,1,2),(3,6,5)
D.
(-1,3,8),(-2,0,5),(2,1,9)
【单选题】已知4阶方阵A=[α 1 ,α 2 ,α 3 ,α 4 ],α 1 ,α 2 ,α 3 ,α 4 均为四维列向量,其中α 1 ,α 2 线性无关,若α 1 +2α 2 -α 3 =β,α 1 +α 2 +α 3 +α 4 =β,2α 1 +3α 2 +α 3 +2α 4 =β,k 1 ,k 2 为任意常数,那么Ax=β的通解为
A.
B.
A. 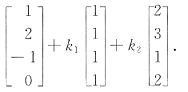
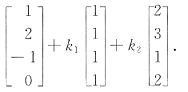
C.
B. 

D.
C. 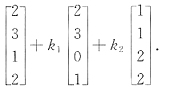
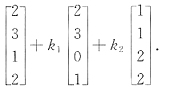
E.
D. 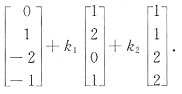
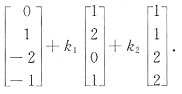
【单选题】设 a , b 是一组非正交的基底,为得到正交基底,可在集合 { a +t b |t∈R} 中找一个向量与 a 组成一组正交基底,根据上述要求,若 a =(1,2) , b =(2,3) ,则t的值为( )
A.
- 3 8
B.
- 5 11
C.
- 5 8
D.
- 7 9

参考解析:


AI解析
重新生成

题目纠错 0
发布

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





