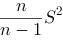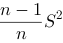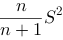创建自己的小题库
搜索
【单选题】
设总体X服从指数分布，概率密度为（）。其中λ未知。如果取得样本观察值为X1，X2，…，X，样本均值为X，则参数λ的极大似然估计是（）。
A.
['x5
B.
C.
n
D.
手机使用
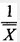
分享
复制链接
新浪微博
分享QQ
微信扫一扫
反馈
收藏
举报参考答案：
举一反三
【单选题】一组免赔额为5的保单赔付样本为：6、7、7、9、11、17、21、34。假设初始损失额服从指数分布，则参数θ的极大似然估计为( )。
A.
12
B.
11
C.
13
D.
14
E.
15
【单选题】某班级学生的年龄是右偏的，均值为19岁，标准差为2.5。如果采用重复抽样的方法从该班抽取容量为100的样本，那么样本均值的分布为（）。
A.
均值为19，标准差为2.5的正态分布
B.
均值为19，标准差为0.25的正态分布
C.
均值为19，标准差为2.5的右偏分布
D.
均值为19，标准差为0.25的右偏分布
【判断题】设总体X的分布律为P(X=0)=θ, P(X=1)=P(X=2)=(1-θ)/2，其中0<θ<1为待估未知参数。设【图片】是简单随机样本。令T为【图片】中0所占的比例, 则T是θ的极大似然估计.
A.
正确
B.
错误
相关题目：
【单选题】一组免赔额为5的保单赔付样本为：6、7、7、9、11、17、21、34。假设初始损失额服从指数分布，则参数θ的极大似然估计为( )。
A.
12
B.
11
C.
13
D.
14
E.
15
【单选题】某班级学生的年龄是右偏的，均值为19岁，标准差为2.5。如果采用重复抽样的方法从该班抽取容量为100的样本，那么样本均值的分布为（）。
A.
均值为19，标准差为2.5的正态分布
B.
均值为19，标准差为0.25的正态分布
C.
均值为19，标准差为2.5的右偏分布
D.
均值为19，标准差为0.25的右偏分布
【判断题】设总体X的分布律为P(X=0)=θ, P(X=1)=P(X=2)=(1-θ)/2，其中0<θ<1为待估未知参数。设【图片】是简单随机样本。令T为【图片】中0所占的比例, 则T是θ的极大似然估计.
A.
正确
B.
错误
参考解析：
AI解析
重新生成
题目纠错 0
发布
