
创建自己的小题库
搜索
【简答题】


若
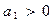 、
、
 ,
,
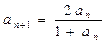
 (1)求证:
(1)求证:
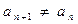 ; (2)令
; (2)令
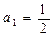 ,写出
,写出
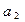 、
、
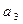 、
、
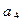 、
、
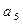 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式
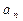 ; (3)证明:存在不等于零的常数p,使
; (3)证明:存在不等于零的常数p,使
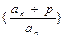 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.

 分享
分享
 反馈
反馈 收藏
收藏 举报
举报参考答案:


举一反三
【简答题】设{an}为公比q>1的等比数列,若a2009和a2010是方程4x2-8x+3=0的两根,则a2011+a2012=( )
A.
18
B.
10
C.
25
D.
9
【单选题】数列{an}的前n项和Sn=3n-c,则c=1是数列{an}为等比数列的( )
A.
充分非必要条件
B.
必要非充分条件
C.
充分必要条件
D.
既非充分又非必要条件

相关题目:
【简答题】设{an}为公比q>1的等比数列,若a2009和a2010是方程4x2-8x+3=0的两根,则a2011+a2012=( )
A.
18
B.
10
C.
25
D.
9
【单选题】数列{an}的前n项和Sn=3n-c,则c=1是数列{an}为等比数列的( )
A.
充分非必要条件
B.
必要非充分条件
C.
充分必要条件
D.
既非充分又非必要条件

参考解析:


AI解析
重新生成

题目纠错 0
发布

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





