
创建自己的小题库
搜索
参考答案:


举一反三
【单选题】设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,a⊥c,|a|=|c|,则|b·c|的值一定等于[ ]
A.
以a,b为两边的三角形面积
B.
以b,c为两边的三角形面积
C.
以a,b为邻边的平行四边形的面积
D.
以b,c为邻边的平行四边形的面积
【简答题】已知 a 、 b 为两个非零向量,有以下命题:① a 2= b 2 ② a • b = b 2 ③| a |=| b |且 a ∥ b ,其中可以作 a = b 的必...
A.
②
B.
①③
C.
②③
D.
①②③
【单选题】已知非零向量、满足向量+与向量-的夹角为,那么下列结论中一定成立的是( )
A.
 =
=

 =
=

B.
|
 |=|
|=|
 |,
|,
 |=|
|=|
 |,
|,C.
 ⊥
⊥

 ⊥
⊥

D.
 ∥
∥

 ∥
∥

【单选题】若一个栈以向量VE1…n]存储,初始栈顶指针top为n+1,则下列X进栈的操作正确的是( )。
A.
top=top+1;V[top]=X
B.
VEtop]=x;top=top+1
C.
top=top一1;V[top]=X
D.
V[top]=x;top=top一1
【单选题】设 是两个非零向量,则下列结论不正确的是
A.
若存在一个实数
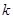 满足
满足
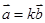 ,则
,则
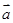 与
与
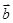 共线
共线
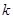 满足
满足
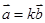 ,则
,则
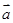 与
与
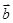 共线
共线B.
若
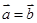 ,则
,则
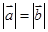
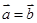 ,则
,则
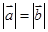
C.
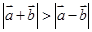
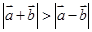
D.
若
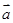 与
与
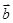 为两个方向相同的向量,则
为两个方向相同的向量,则
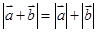
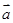 与
与
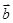 为两个方向相同的向量,则
为两个方向相同的向量,则
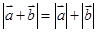

相关题目:
【单选题】设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,a⊥c,|a|=|c|,则|b·c|的值一定等于[ ]
A.
以a,b为两边的三角形面积
B.
以b,c为两边的三角形面积
C.
以a,b为邻边的平行四边形的面积
D.
以b,c为邻边的平行四边形的面积
【简答题】已知 a 、 b 为两个非零向量,有以下命题:① a 2= b 2 ② a • b = b 2 ③| a |=| b |且 a ∥ b ,其中可以作 a = b 的必...
A.
②
B.
①③
C.
②③
D.
①②③
【单选题】已知非零向量、满足向量+与向量-的夹角为,那么下列结论中一定成立的是( )
A.
 =
=

 =
=

B.
|
 |=|
|=|
 |,
|,
 |=|
|=|
 |,
|,C.
 ⊥
⊥

 ⊥
⊥

D.
 ∥
∥

 ∥
∥

【单选题】若一个栈以向量VE1…n]存储,初始栈顶指针top为n+1,则下列X进栈的操作正确的是( )。
A.
top=top+1;V[top]=X
B.
VEtop]=x;top=top+1
C.
top=top一1;V[top]=X
D.
V[top]=x;top=top一1
【单选题】设 是两个非零向量,则下列结论不正确的是
A.
若存在一个实数
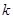 满足
满足
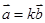 ,则
,则
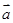 与
与
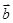 共线
共线
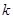 满足
满足
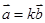 ,则
,则
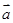 与
与
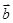 共线
共线B.
若
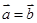 ,则
,则
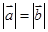
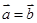 ,则
,则
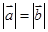
C.
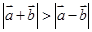
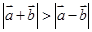
D.
若
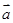 与
与
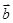 为两个方向相同的向量,则
为两个方向相同的向量,则
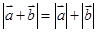
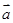 与
与
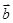 为两个方向相同的向量,则
为两个方向相同的向量,则
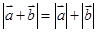

参考解析:


AI解析
重新生成

题目纠错 0
发布


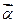 、
、
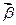 满足
满足
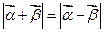 ,证明:
,证明:

 分享
分享 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫 反馈
反馈 收藏
收藏 举报
举报





