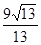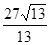创建自己的小题库
搜索
【简答题】


已知二面角α-l-β的大小为30°,m、n为异面直线,m⊥平面α,n⊥平面β,则m、n所成的角为______.

 分享
分享
 反馈
反馈 收藏
收藏 举报
举报参考答案:


举一反三
【单选题】黑龙江地区的广大尚未开垦的荒芜地域都被泛指为(),这是广义上的“北大荒”。随着岁月的更迭,北大荒的范围逐渐缩小为黑龙江省松嫩平原和三江平原一代的千里荒原。
A.
“北大荒”
B.
“黑土地”
C.
“大荒北”
D.
“土中之王”
【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
【单选题】如下图所示,去医院治牙,静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角g,若此人所受重力为G,则椅子各部分对他的作用力的合力大小为 :
A.
G
B.
Gsing
C.
Gcosg
D.
Gtang
【单选题】两条异面直线指的是( )
A.
空间中不相交的两条直线;
B.
分别位于两个不同平面内的两条直线;
C.
某一平面内的一条直线和这个平面外的一条直线;
D.
不 同在任何一个平面内的两条直线.
【单选题】在成人心肺复苏中,潮气量大小为:
A.
500-600ml
B.
600-700ml
C.
400-500ml
D.
800-1000ml
【多选题】多选 一物体作竖直上抛运动(不计空气阻力),初速度为30m/s,当它位移大小为25m时,经历时间为(g=10m/s2)( )
A.
1s
B.
2s
C.
5s
D.
3s
【单选题】类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的下列性质,你认为比较恰当的是 ①各棱长相等,同一顶点上的任两条棱的夹角相等;②各个面是全等的正三角形,相邻的两个面所成的二面角相等;③各个面都是全等的正三角形,同一顶点的任两条棱的夹角相等;④各棱长相等,相邻两个面所成的二面角相等。 [ ]
A.
①④
B.
①②
C.
①②③
D.
③

相关题目:
【单选题】黑龙江地区的广大尚未开垦的荒芜地域都被泛指为(),这是广义上的“北大荒”。随着岁月的更迭,北大荒的范围逐渐缩小为黑龙江省松嫩平原和三江平原一代的千里荒原。
A.
“北大荒”
B.
“黑土地”
C.
“大荒北”
D.
“土中之王”
【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
【单选题】如下图所示,去医院治牙,静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角g,若此人所受重力为G,则椅子各部分对他的作用力的合力大小为 :
A.
G
B.
Gsing
C.
Gcosg
D.
Gtang
【单选题】两条异面直线指的是( )
A.
空间中不相交的两条直线;
B.
分别位于两个不同平面内的两条直线;
C.
某一平面内的一条直线和这个平面外的一条直线;
D.
不 同在任何一个平面内的两条直线.
【单选题】在成人心肺复苏中,潮气量大小为:
A.
500-600ml
B.
600-700ml
C.
400-500ml
D.
800-1000ml
【多选题】多选 一物体作竖直上抛运动(不计空气阻力),初速度为30m/s,当它位移大小为25m时,经历时间为(g=10m/s2)( )
A.
1s
B.
2s
C.
5s
D.
3s
【单选题】类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的下列性质,你认为比较恰当的是 ①各棱长相等,同一顶点上的任两条棱的夹角相等;②各个面是全等的正三角形,相邻的两个面所成的二面角相等;③各个面都是全等的正三角形,同一顶点的任两条棱的夹角相等;④各棱长相等,相邻两个面所成的二面角相等。 [ ]
A.
①④
B.
①②
C.
①②③
D.
③

参考解析:


AI解析
重新生成

题目纠错 0
发布

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫