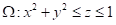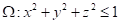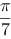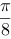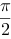创建自己的小题库
搜索
【简答题】
将下列三重积分化为直角坐标系下的三次积分 设 是由双曲抛物面 ,平面 围成的闭区域, 则
手机使用
分享
复制链接
新浪微博
分享QQ
微信扫一扫
反馈
收藏
举报参考答案：
举一反三
【单选题】设空间区域$\Omega =\left\{ (x,y,z)|\sqrt{{{x}^{2}}+{{y}^{2}}}\le z\le 1 \right\}$，则三重积分$\iiint\limits {\Omega }{\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}x\text{d}y\text{d}z}=$ ( ).
A.
$\text{ }\!\!\pi\!\!\text{ }$
B.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$
C.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$
D.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$
相关题目：
【单选题】设空间区域$\Omega =\left\{ (x,y,z)|\sqrt{{{x}^{2}}+{{y}^{2}}}\le z\le 1 \right\}$，则三重积分$\iiint\limits {\Omega }{\sqrt{{{x}^{2}}+{{y}^{2}}}\text{d}x\text{d}y\text{d}z}=$ ( ).
A.
$\text{ }\!\!\pi\!\!\text{ }$
B.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$
C.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$
D.
$\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$
参考解析：
AI解析
重新生成
题目纠错 0
发布
