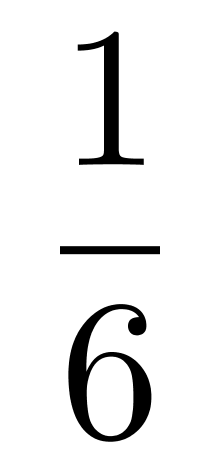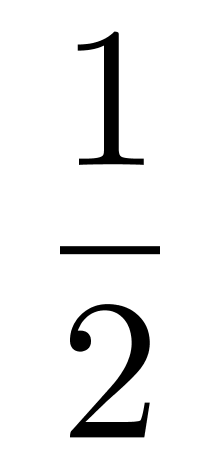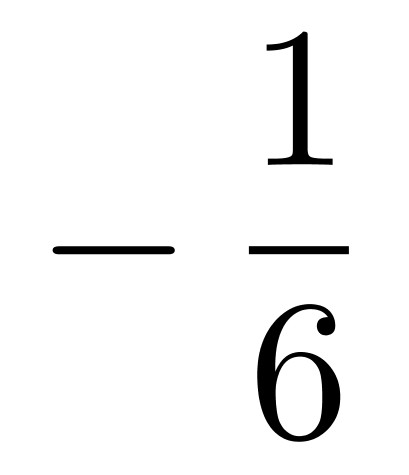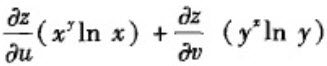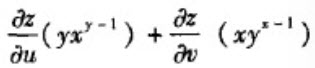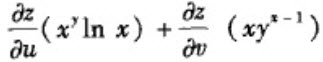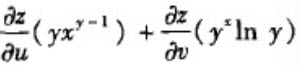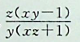创建自己的小题库
搜索
【简答题】


设X=C1[a,b],即为[a,b]上所有连续可微函数空间。对x∈Y,令
‖x‖=‖x‖∞+‖x'‖∞ ‖x‖1=|x(a)|+‖x'‖∞,
其中x'是x导数。证明X赋有上面任一个范数都是Banach空间。再证明对X中所有x,
‖x‖1≤‖x‖≤(b-a+1)‖x‖1,
且常数b=a+1是最佳的。

 分享
分享
 反馈
反馈 收藏
收藏 举报
举报参考答案:


举一反三
【单选题】设z=f(x,y)是由F(x+2z,y+3z)=0确定,F是可微函数,2F" u +3F" v ≠0,其中u=x+2z,v=y+3z,则 等于______
A.
B.
A. 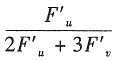
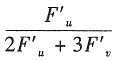
C.
B. 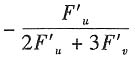
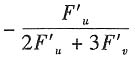
D.
C. 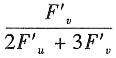
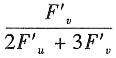
E.
D. 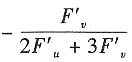
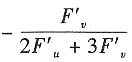

相关题目:
【单选题】设z=f(x,y)是由F(x+2z,y+3z)=0确定,F是可微函数,2F" u +3F" v ≠0,其中u=x+2z,v=y+3z,则 等于______
A.
B.
A. 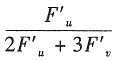
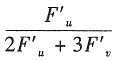
C.
B. 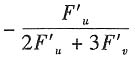
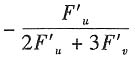
D.
C. 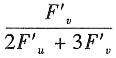
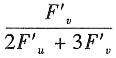
E.
D. 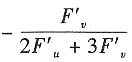
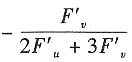

参考解析:


AI解析
重新生成

题目纠错 0
发布

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫