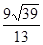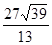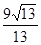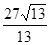大学职业搜题刷题APP
下载APP
首页
课程
题库模板
Word题库模板
Excel题库模板
PDF题库模板
医考护考模板
答案在末尾模板
答案分章节末尾模板
题库创建教程
创建题库
登录
logo - 刷刷题
创建自己的小题库
搜索
【简答题】

下列命题正确的个数为（　　）①斜线与它在平面内的射影所成的角是这条斜线和这个平面内所有直线所成的角的最小角．②二面角α-l-β的平面角是过棱l上任一点O，分别在两个半平面内任意两条射线OA，OB所成角的∠AOB的最大角．③如果一条直线和一个平面的一条斜线垂直，那么它也和这条斜线在这个平面内的射影垂直．④设A是空间一点，

题目标签：二面角半平面平面角
如何将EXCEL生成题库手机刷题
相关题库：真命题、假命题题库 >
手机使用
分享
复制链接
新浪微博
分享QQ
微信扫一扫
微信内点击右上角“…”即可分享
反馈
收藏 - 刷刷题收藏
举报
参考答案：
举一反三

【简答题】已知四棱锥P-ABCD中，P在底面的射影O是四边形ABCD内切圆的圆心，给定的四个命题：①各侧面和底面所成的二面角相等；②点O到各侧面的距离相等；③侧棱PA=PB=PC=PD；④△PAB、△PBC、△PCD、△PDA的面积之比是AB：BC：CD：DA．其中正确的是（　　） A．①②③ B．②③④ C．①②④ D．①③④
查看完整题目与答案
高中数学>真命题、假命题考试题目

【简答题】(本小题满分12分) 如图，直三棱柱 中， AB=1， ，∠ ABC=60 . (1)证明： ； （2）求二面角 A— — B的余弦值。
查看完整题目与答案
高中数学>柱、锥、台、球的结构特征考试题目

【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
查看完整题目与答案

【简答题】（12分）如图所示，已知三棱柱ABC- 的底面边长均为2，侧棱 的长为2且与底面ABC所成角为 ，且侧面 垂直于底面ABC． （1）求二面角 的正切值的大小； （2）若其余条件不变，只改变侧棱的长度，当侧棱 的长度为多长时，可使面 和底面垂直．
查看完整题目与答案

【单选题】在矩形 中， 是 的中点，沿 将 折起，使二面角 为60°，则四棱锥 的体积是
A.
B.
C.
D.
查看完整题目与答案
高中数学>空间几何体的三视图考试题目

【简答题】如图，在四面体ABCD中，平面ABC⊥平面ACD，AB⊥BC，AD=CD，∠CAD=30°。 （1）若AD=2，AB=2BC，求四面体ABCD的体积； （2）若二面角C-AB-D为60°，求异面直线AD与BC所成角的余弦值。
查看完整题目与答案
高中数学>柱体、椎体、台体的表面积与体积考试题目

【简答题】将边长为a的正边形ABCD沿对角线AC折成60°的二面角后，B，D两点之间的距离等于（ ）。
查看完整题目与答案

【简答题】(本题满分12分)下面的一组图形为某一四棱锥S-ABCD的侧面与底面。 （1）请画出四棱锥S-ABCD的直观图，是否存在一条侧棱垂直于底面？如果存在，请给出证明；如果不存在，请说明理由； （2）若SA 面ABCD，E为AB中点，求二面角E-SC-D的大小； （3）求点D到面S EC的距离。
查看完整题目与答案
高中数学>空间几何体的三视图考试题目

【单选题】类比平面内正三角形的“三边相等，三内角相等”的性质，可推知正四面体的下列性质，你认为比较恰当的是 ①各棱长相等，同一顶点上的任两条棱的夹角相等；②各个面是全等的正三角形，相邻的两个面所成的二面角相等；③各个面都是全等的正三角形，同一顶点的任两条棱的夹角相等；④各棱长相等，相邻两个面所成的二面角相等。 [ ]
A.
①④
B.
①②
C.
①②③
D.
③
查看完整题目与答案
高中数学>球与正方体、长方体、四面体组合的结构特征考试题目

【简答题】如图，在三棱柱ABC﹣A1B1C1中，侧面BB1C1C、BB1A1A为全等的矩形，并且AB=1，BB1=2，AB⊥侧面BB1C1C，D为棱C1C上异于C、C1的一点，且DB⊥DA1． （1）求证：B1D⊥平面ABD； （2）求二面角A﹣DB1﹣A1的余弦值．
查看完整题目与答案
高中数学>二面角考试题目
相关题目：
【简答题】已知四棱锥P-ABCD中，P在底面的射影O是四边形ABCD内切圆的圆心，给定的四个命题：①各侧面和底面所成的二面角相等；②点O到各侧面的距离相等；③侧棱PA=PB=PC=PD；④△PAB、△PBC、△PCD、△PDA的面积之比是AB：BC：CD：DA．其中正确的是（　　） A．①②③ B．②③④ C．①②④ D．①③④
查看完整题目与答案
【简答题】(本小题满分12分) 如图，直三棱柱 中， AB=1， ，∠ ABC=60 . (1)证明： ； （2）求二面角 A— — B的余弦值。
查看完整题目与答案
【单选题】二面角是指( )
A.
两个平面所组成的角
B.
经过同一条直线出发的两个半平面所组成的图形
C.
从一条直线出发的两个半平面所组成的图形
D.
两个平面所夹的不大于90°的角
查看完整题目与答案
【简答题】（12分）如图所示，已知三棱柱ABC- 的底面边长均为2，侧棱 的长为2且与底面ABC所成角为 ，且侧面 垂直于底面ABC． （1）求二面角 的正切值的大小； （2）若其余条件不变，只改变侧棱的长度，当侧棱 的长度为多长时，可使面 和底面垂直．
查看完整题目与答案
【单选题】在矩形 中， 是 的中点，沿 将 折起，使二面角 为60°，则四棱锥 的体积是
A.
B.
C.
D.
查看完整题目与答案
【简答题】如图，在四面体ABCD中，平面ABC⊥平面ACD，AB⊥BC，AD=CD，∠CAD=30°。 （1）若AD=2，AB=2BC，求四面体ABCD的体积； （2）若二面角C-AB-D为60°，求异面直线AD与BC所成角的余弦值。
查看完整题目与答案
【简答题】将边长为a的正边形ABCD沿对角线AC折成60°的二面角后，B，D两点之间的距离等于（ ）。
查看完整题目与答案
【简答题】(本题满分12分)下面的一组图形为某一四棱锥S-ABCD的侧面与底面。 （1）请画出四棱锥S-ABCD的直观图，是否存在一条侧棱垂直于底面？如果存在，请给出证明；如果不存在，请说明理由； （2）若SA 面ABCD，E为AB中点，求二面角E-SC-D的大小； （3）求点D到面S EC的距离。
查看完整题目与答案
【单选题】类比平面内正三角形的“三边相等，三内角相等”的性质，可推知正四面体的下列性质，你认为比较恰当的是 ①各棱长相等，同一顶点上的任两条棱的夹角相等；②各个面是全等的正三角形，相邻的两个面所成的二面角相等；③各个面都是全等的正三角形，同一顶点的任两条棱的夹角相等；④各棱长相等，相邻两个面所成的二面角相等。 [ ]
A.
①④
B.
①②
C.
①②③
D.
③
查看完整题目与答案
【简答题】如图，在三棱柱ABC﹣A1B1C1中，侧面BB1C1C、BB1A1A为全等的矩形，并且AB=1，BB1=2，AB⊥侧面BB1C1C，D为棱C1C上异于C、C1的一点，且DB⊥DA1． （1）求证：B1D⊥平面ABD； （2）求二面角A﹣DB1﹣A1的余弦值．
查看完整题目与答案
刷刷题-刷题-导入试题 - 刷刷题
参考解析：
AI解析
重新生成
题目纠错 0
发布
刷刷题-刷题-导入试题 - 刷刷题刷刷题-刷题-导入试题 - 刷刷题刷刷题-刷题-导入试题 - 刷刷题
刷刷题-刷题-导入试题 - 刷刷题
刷刷题-刷题-导入试题 - 刷刷题
刷刷题-单词鸭