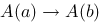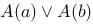创建自己的小题库
搜索
【判断题】
论域的不同,命题符号化的形式可能不一样。
A.
正确
B.
错误
手机使用
分享
复制链接
新浪微博
分享QQ
微信扫一扫
反馈
收藏
举报参考答案：
举一反三
【单选题】设x→a时，f（x）与g（x）分别是x—a的n阶与m阶无穷小，则下列命题中，正确的个数是（ ）①f（x）g（x）是x—a的n+m阶无穷小。②若n＞m，则是x一a的n—m阶无穷小。③若n≤m，则f（x）+g（x）是x—a的n阶无穷小。
A.
1
B.
2
C.
3
D.
0
【单选题】（ ）从整体上规定某门课程的性质及其在课程体系中的地位，是教材编写、教学、评估和考试命题的依据，也是国家管理和评价课程的基础。
A.
课程标准
B.
教学原则
C.
教学计划
D.
课程方案
【单选题】下列四个命题中可能成立的一个是（ ）
A.
sinα=12，且cosα=12
B.
sinα=0，且cosα=-1
C.
tanα=1，且cosα=-1
D.
α是第二象限角时，tanα=-sinαcosα
【单选题】用反证法证明命题：若P则q ，其第一步是反设命题的结论不成立，这个正确的反设是
A.
若P则非q
B.
若非P则q
C.
非P
D.
非q
相关题目：
【单选题】设x→a时，f（x）与g（x）分别是x—a的n阶与m阶无穷小，则下列命题中，正确的个数是（ ）①f（x）g（x）是x—a的n+m阶无穷小。②若n＞m，则是x一a的n—m阶无穷小。③若n≤m，则f（x）+g（x）是x—a的n阶无穷小。
A.
1
B.
2
C.
3
D.
0
【单选题】（ ）从整体上规定某门课程的性质及其在课程体系中的地位，是教材编写、教学、评估和考试命题的依据，也是国家管理和评价课程的基础。
A.
课程标准
B.
教学原则
C.
教学计划
D.
课程方案
【单选题】下列四个命题中可能成立的一个是（ ）
A.
sinα=12，且cosα=12
B.
sinα=0，且cosα=-1
C.
tanα=1，且cosα=-1
D.
α是第二象限角时，tanα=-sinαcosα
【单选题】用反证法证明命题：若P则q ，其第一步是反设命题的结论不成立，这个正确的反设是
A.
若P则非q
B.
若非P则q
C.
非P
D.
非q
参考解析：
AI解析
重新生成
题目纠错 0
发布
