
创建自己的小题库
搜索
【简答题】


(13分)
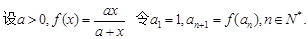 (1)写出 a2, a3, a4的值,并猜想数列{ an}的通项公式; (2)用数学归纳法证明你的结论;
(1)写出 a2, a3, a4的值,并猜想数列{ an}的通项公式; (2)用数学归纳法证明你的结论;

 分享
分享
 反馈
反馈 收藏
收藏 举报
举报参考答案:


举一反三
【单选题】利用数学归纳法证明不等式1n+1+1n+2+…+1n+n>12(n>1,n?N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果为( )
A.
12(k+1)
B.
12k+1+12(k+1)
【简答题】已知函数f(x)=-2x+2( 1 2 ≤x≤1)的反函数为y=g(x),a1=1,a2=g(a1),a3=g(a2),…,an=g(an-1),…,求数列{an}的通项公式及前n项和Sn.
【多选题】下列选项中,运用归纳法进行行业分析的步骤是()。
A.
收集相关资料
B.
根据实际观察结果找出一个最能代表或者描述资料特点的模式
C.
对假设和实际观察结果进行比较
D.
运用归纳法考察数量之间的关系后,最终得到了一个趋势性的结果

相关题目:
【单选题】利用数学归纳法证明不等式1n+1+1n+2+…+1n+n>12(n>1,n?N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果为( )
A.
12(k+1)
B.
12k+1+12(k+1)
【简答题】已知函数f(x)=-2x+2( 1 2 ≤x≤1)的反函数为y=g(x),a1=1,a2=g(a1),a3=g(a2),…,an=g(an-1),…,求数列{an}的通项公式及前n项和Sn.
【多选题】下列选项中,运用归纳法进行行业分析的步骤是()。
A.
收集相关资料
B.
根据实际观察结果找出一个最能代表或者描述资料特点的模式
C.
对假设和实际观察结果进行比较
D.
运用归纳法考察数量之间的关系后,最终得到了一个趋势性的结果

参考解析:


AI解析
重新生成

题目纠错 0
发布

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





