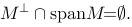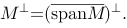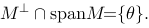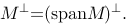大学职业搜题刷题APP
下载APP
首页
课程
题库模板
Word题库模板
Excel题库模板
PDF题库模板
医考护考模板
答案在末尾模板
答案分章节末尾模板
题库创建教程
创建题库
登录
logo - 刷刷题
创建自己的小题库
搜索
【简答题】

设z为内积空间X一固定元。求证：
f(x)=＜x，z＞，x∈X
定义了X上范数为‖z‖的有界线性泛函证明若映射X→X'，z→f为满射，则X必为Hilbert空间。

题目标签：积空间内积空间线性泛函
如何将EXCEL生成题库手机刷题
如何制作自己的在线小题库 >
手机使用
分享
复制链接
新浪微博
分享QQ
微信扫一扫
微信内点击右上角“…”即可分享
反馈
收藏 - 刷刷题收藏
举报
参考答案：
举一反三

【简答题】设M与N是内积空间X中的两个子集证明若M⊆M⊥
查看完整题目与答案

【简答题】若M为内积空间X的非空子集。求证：M的正交补为X的闭子空间。
查看完整题目与答案

【判断题】设 是拓扑空间 中的开集 , , 则 是积空间 中的开集 .
A.
正确
B.
错误
查看完整题目与答案

【多选题】内积空间一定是（ ）.
A.
线性空间
B.
赋范空间
C.
距离空间
D.
N维欧氏空间
查看完整题目与答案

【判断题】完备的内积空间被称为Hilbert空间。 （ ）
A.
正确
B.
错误
查看完整题目与答案

【简答题】设Xi和Yi(i=1，2)都是Banach空间，X=X1×X2，Y=Y1×Y2为积空间，设，线性算子T：X→Y定义为T(x1，x2)=(T1x1,T2x2),(x1,x2)∈X.证明：
查看完整题目与答案

【简答题】内积空间 中的向量 线性无关的充要条件是Gram矩阵
查看完整题目与答案

【判断题】ch3::20191117:最佳平方逼近 若 是内积空间,则在2范数意义下, 在有限空间 中的最佳逼近元是 在 上的正交投影.
A.
正确
B.
错误
查看完整题目与答案

【简答题】证明：内积空间X中两个向量x，y垂直的充要条件是：对一切数α，成立||x+αy||≥||x||。
查看完整题目与答案

【单选题】内积空间中线性无关元素确定的Gram矩阵是实对称正定矩阵 （ ）
A.
对
B.
错
查看完整题目与答案

【简答题】举例说明内积空间中完全规范正交系不一定是完备的。
查看完整题目与答案

【简答题】完备的內积空间叫做 空间
查看完整题目与答案

【简答题】设X是内积空间，证明：由内积诱导的范数满足平行四边形公式．
查看完整题目与答案

【单选题】设M是内积空间H的子集，则以下选项中错误的是（ ）.
A.
B.
C.
D.
查看完整题目与答案

【判断题】内积空间的正交基一定是正交系，反之不成立.
A.
正确
B.
错误
查看完整题目与答案

【多选题】实内积空间上的内积满足（ ）.
A.
对称性
B.
非负性
C.
对第一变元的线性性质
D.
对第二变元的线性性质
查看完整题目与答案

【判断题】任意一个内积空间都可以定义范数使之成为赋范线性空间。
A.
正确
B.
错误
查看完整题目与答案

【简答题】设x，y，z为内积空间X中的元。求证Appolonius等式：t‖x-y‖2+(1-t)‖x-z‖2=‖x-u‖2+t(1-t)‖y-z‖2，其中u=ty+(1-t)z，。由此推出
查看完整题目与答案

【简答题】设X是一个内积空间，(.,.)为内积， 是x的一个n空间．f∈x， 对 ，1≤i，j≤n，b i =(f， )，1≤i≤n，矩阵A=[a ij ]，b=(b 1 ，b 2 ，…，b n ) T ． 1)证明：线性方程组Ax=b存在唯一解； 2)如果P满足‖f-p‖= ‖f-q‖证明：c 1 ，c 2 ，…，c n 是线性方程组Ax=b的解．
查看完整题目与答案

【简答题】设是内积空间，则x⊥y的充分必要条件是对任何数α有‖x+αy‖≥‖x-αy‖
查看完整题目与答案
相关题目：
【简答题】设M与N是内积空间X中的两个子集证明若M⊆M⊥
查看完整题目与答案
【简答题】若M为内积空间X的非空子集。求证：M的正交补为X的闭子空间。
查看完整题目与答案
【判断题】设 是拓扑空间 中的开集 , , 则 是积空间 中的开集 .
A.
正确
B.
错误
查看完整题目与答案
【多选题】内积空间一定是（ ）.
A.
线性空间
B.
赋范空间
C.
距离空间
D.
N维欧氏空间
查看完整题目与答案
【判断题】完备的内积空间被称为Hilbert空间。 （ ）
A.
正确
B.
错误
查看完整题目与答案
【简答题】设Xi和Yi(i=1，2)都是Banach空间，X=X1×X2，Y=Y1×Y2为积空间，设，线性算子T：X→Y定义为T(x1，x2)=(T1x1,T2x2),(x1,x2)∈X.证明：
查看完整题目与答案
【简答题】内积空间 中的向量 线性无关的充要条件是Gram矩阵
查看完整题目与答案
【判断题】ch3::20191117:最佳平方逼近 若 是内积空间,则在2范数意义下, 在有限空间 中的最佳逼近元是 在 上的正交投影.
A.
正确
B.
错误
查看完整题目与答案
【简答题】证明：内积空间X中两个向量x，y垂直的充要条件是：对一切数α，成立||x+αy||≥||x||。
查看完整题目与答案
【单选题】内积空间中线性无关元素确定的Gram矩阵是实对称正定矩阵 （ ）
A.
对
B.
错
查看完整题目与答案
【简答题】举例说明内积空间中完全规范正交系不一定是完备的。
查看完整题目与答案
【简答题】完备的內积空间叫做 空间
查看完整题目与答案
【简答题】设X是内积空间，证明：由内积诱导的范数满足平行四边形公式．
查看完整题目与答案
【单选题】设M是内积空间H的子集，则以下选项中错误的是（ ）.
A.
B.
C.
D.
查看完整题目与答案
【判断题】内积空间的正交基一定是正交系，反之不成立.
A.
正确
B.
错误
查看完整题目与答案
【多选题】实内积空间上的内积满足（ ）.
A.
对称性
B.
非负性
C.
对第一变元的线性性质
D.
对第二变元的线性性质
查看完整题目与答案
【判断题】任意一个内积空间都可以定义范数使之成为赋范线性空间。
A.
正确
B.
错误
查看完整题目与答案
【简答题】设x，y，z为内积空间X中的元。求证Appolonius等式：t‖x-y‖2+(1-t)‖x-z‖2=‖x-u‖2+t(1-t)‖y-z‖2，其中u=ty+(1-t)z，。由此推出
查看完整题目与答案
【简答题】设X是一个内积空间，(.,.)为内积， 是x的一个n空间．f∈x， 对 ，1≤i，j≤n，b i =(f， )，1≤i≤n，矩阵A=[a ij ]，b=(b 1 ，b 2 ，…，b n ) T ． 1)证明：线性方程组Ax=b存在唯一解； 2)如果P满足‖f-p‖= ‖f-q‖证明：c 1 ，c 2 ，…，c n 是线性方程组Ax=b的解．
查看完整题目与答案
【简答题】设是内积空间，则x⊥y的充分必要条件是对任何数α有‖x+αy‖≥‖x-αy‖
查看完整题目与答案
刷刷题-刷题-导入试题 - 刷刷题
参考解析：
AI解析
重新生成
题目纠错 0
发布
刷刷题-刷题-导入试题 - 刷刷题刷刷题-刷题-导入试题 - 刷刷题刷刷题-刷题-导入试题 - 刷刷题
刷刷题-刷题-导入试题 - 刷刷题
刷刷题-刷题-导入试题 - 刷刷题
刷刷题-单词鸭